In Part 3 (July/August issue) we determined the height of our structures and the strength of our structures and foundations to comply with the National Electrical Safety Code® (NESC®). The last step in the design of a high-voltage overhead line up to 50 kV to comply with the NESC is to design the guying. Stringing conductors between poles puts tension on the poles. Though poles and foundations can be designed with enough strength to hold the tension, guying is much more economical.
Dead-End Guying
To understand the principles of anchor guying, let’s look at a simple example. Consider a single 250 foot span of 477 AAC “Cosmos” conductor strung between two poles at a stringing tension of 1410 pounds at 60 degrees F. The conductor is dead-ended on each pole at a height of 35 feet.
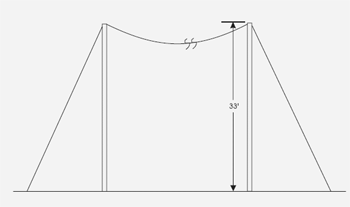
To prevent the poles from breaking at or near the ground line and to prevent the poles from kicking out (tipping over due to foundation failure), we need to install an anchor guy on each pole
The “longitudinal load” or force on the pole the anchor guy must hold is the final tension of the conductor under the conditions specified by Table 250-1 for the applicable loading district. Referring back to the heavy loading district Sag/Tension table for 477 AAC presented in Part 2 (May/June issue), the final tension of the conductor at 0 degrees F. with 1/2 inch of ice and 4 lb./sq. ft. wind pressure is 3601 pounds. Let’s assume we will install our anchor in the ground about 20 feet from the pole. This distance is called the guy lead.
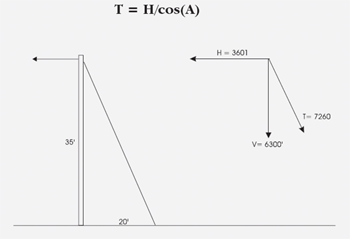
The tension in the guy wire and the anchor is the longitudinal load on the pole due to the conductor “H” divided by the cosine of the angle “A”.
The angle “A” is the arctangent of the guy attachment height divided by the guy lead.
A = tan-1(35’/20′)
A = 66.9 degrees
T = 3601 lb / cos 66.9
T = 3601 / .496
T = 7260 pounds
For grade B and C construction, the rated strength of the guy wire and the anchor must exceed the guy tension “T” multiplied by the appropriate safety factors specified in Rules 261 C and B, respectively. For a discussion of Safety Factors, see my article “Strong Enough to be Safe” in the January/February issue. The rated strength of the anchor must take into consideration the type of soil in which it is installed.
The vertical force “V” on the pole due to the anchor is the tension in the guy wire “T” multiplied by the sine of the angle “A”.
V = T x sin(A)
V = 7260 x sin 66.9
V = 7260 x .867
V = 6300 pounds
For grades B and C construction, the vertical strength of the pole and its’ foundation must exceed the vertical force on the pole “V” multiplied by the appropriate safety factor specified in Rules 261A and B, respectively, or the pole may buckle or sink. The shorter the guy lead, the higher the tension in the guy wire and anchor and the higher the vertical force on the pole. Using a shortlead increases the probability of the anchor slipping (pulling out) or the pole sinking, either of which will cause the pole to lean and the conductors’ sag to increase. The increased sag may cause a clearance violation.
Multi-Span Lines
All the spans of a multi-span line are usually strung at the same time and at the same tension. If all spans are not the same length, this stringing technique complicates the design. If each span is designed separately, the tension of the conductors in each span is a function of the span length, i.e. the longer the span, the higher the tension. If we string the different length spans at the same tension, what stringing tension do we use and what final tension doe we use in the guying calculation? The tensions we are looking for are the tensions of the “Ruling Span”. The Ruling Span is a weighted average span. The calculation method gives longer spans more effect on the average. The Ruling Span is the square root of the sum of each span cubed divided by the sum of the spans.
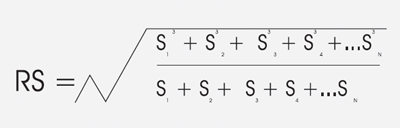
Where S1 through SN are the individual span lengths and S13 = S1 x S1 x S1
The conductor tension we use for the guying calculation must come from a sag/tension calculation based on the Ruling Span length.
Let’s look at a common example of a three-phase vertical dead-end structure shown below:
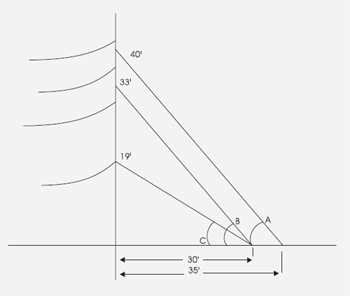
In this example, the top three conductors are 477 AAC phase conductors. The bottom conductor is a 1/0 ACSR neutral conductor. The longitudinal load of the phase conductors is divided between the top two guys. The bottom guy holds the longitudinal load of the neutral. The tension in the top guy and its anchor is the longitudinal load of each phase conductor multiplied by three, divided by two and divided by the cosine of the angle “A”.
T = H x 3
2 x cos(A)
A = tan-1(40/35)
A = 54.2 Degrees
T = 3601 x 3
2 x .658
T = 8209 Pounds
The rated strength of the top guy wire and its anchor must exceed the tension “T” multiplied times the appropriate safety factor specified in Rules 261C and B, respectively. The tension in the middle guy wire is calculated similarly except that angle B is different. The tension in the lower guy wire is the longitudinal load of the neutral conductor divided by the cosine of the angle C. The tension in the anchor closest to the pole is the sum of the tensions in the bottom two guy wires.















Find Us on Socials