The more accident investigations I perform, the more I am convinced that a thorough understanding of basic electricity is critical in solving tough cases. In the past twenty years, I have taught basic electricity more than any other subject. A majority of my students are lawyers. In order for them to understand how an electrical accident happened, they must know the basics of electricity.
What Is Electricity?
To answer this question, I first consulted the IEEE Standard 100, The Authoritative Dictionary of IEEE Standards Terms. With nearly 35,000 entries, it doesn’t define the term electricity. Note that back in 1992, IEEE Standard 100 was called the IEEE Standard Dictionary of Electrical and Electronic Terms. I presume that at some time after 1992, the authors of IEEE Standard 100 realized that trying to keep up with all the new electrical and electronic terms was becoming too difficult. Keeping up with the terms used in just the IEEE Standards was within their grasp and control, hence the revised title and scope.
The need for the use of well-defined industry-standard terms in litigation is critical. Don’t be surprised if a definition in IEEE Standard 100 is different from the definition within another standards authority’s publication.
I then consulted The American Heritage Dictionary. “Electricity. The class of physical phenomena arising from the existence and interactions of electric charge.” It sounds like a definition of static electricity. Today, I’m not talking about static electricity. That’s another can of worms. I’m talking about the electricity that makes my refrigerator, TV, air conditioner, and lights work.
As electrical inspectors, we typically speak of electricity using terms like voltage, current, amps, resistance, watts, and watt-hours. The electrically uneducated general public often uses the term electricity in place of the more specific terms with which we are familiar with.
The following are examples of the use of the term electricity by the general public.
“How much electricity is in those wires?”
“The electricity in the stove jumped out and bit me.”
“My TV burned up because you gave me too much electricity.”
Note that if we substitute the term voltage for electricity in the previous three sentences, we immediately have a better understanding of what the person is talking about. When people ask me, “What is electricity?” I tell them that electricity is the presence of voltage.
Why Do Some Materials Conduct Electricity Better Than Others?
A common analogy some people think of when discussing current flowing in a wire is water flowing in a pipe. Though there are some similarities between the two ideas, the conduction of current through a wire is very different from the flow of water within a pipe. Water can flow through a pipe because there is a space inside the pipe filled with air. The water can flow through the pipe by pushing the air out. There is no space inside a wire. The wire is solid metal. So, how does current flow through a wire? All materials known to man are made up of one or a combination of up to 103 elements, as of 1967. You may recall chemistry teachers referring to the Periodic Table, a spreadsheet that listed all the elements by symbol and atomic number. All the elements are made up of atoms.
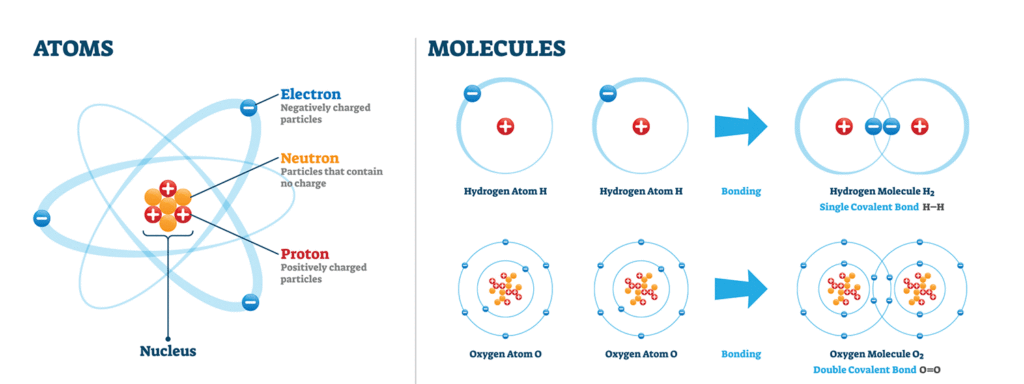
Atoms are so small that we cannot see them, even with the most powerful microscopes. For centuries, scientists have tried to predict what an atom looks like in order to explain its behavior. The image of the atom that works well for me in describing electricity is the Bohr atom. In 1913, a Danish physicist named Niels Bohr described the atom as made up of a nucleus surrounded by electrons.
The nucleus is made up of protons and neutrons. Electrons travel around the nucleus in very specific orbits similar to the planets orbiting around the sun. The maximum number of electrons that can orbit around the nucleus in the closest orbit is two. In the next orbit, the maximum number is eight. In the third orbit, the maximum number is eighteen.
The atomic number of the element is the number of electrons that make up the atoms of the element. Elements that easily conduct current have only a few electrons in the outermost orbit. Current is the motion of electrons from atom to atom within the material.
Current is measured in amperes, amps for short, and abbreviated as A. Though the number of electrons within an atom cannot change, an atom can pass an electron to another atom if it receives one simultaneously. All materials conduct current to some degree. Some conduct better than others.
The four best conductors of current at room temperature are silver, copper, gold, and aluminum. These elements are much more willing to pass on their electrons than other materials. These materials are commonly called conductors because they have very low resistance to passing on electrons.
Materials that do not pass on their electrons easily are called insulators. Their resistance to pass on electrons is very high. Some examples of insulators are dry air, porcelain, glass, rubber, and plastics like PVC and polyethylene. A chamber that has been evacuated, i.e., all or most of the air removed, is a very good insulator because there are no or very few atoms left to pass on their electrons. Materials that fall between conductors and insulators relative to their resistance to passing on electrons are often referred to as semiconductors.
The Circuit
For current to flow within a material, the electrons within the material’s atoms have to be passed on from one atom to the next. To visualize what is happening, let us imagine a straight piece of copper wire six inches long. Let us imagine that the diameter of the wire is the diameter of the atoms within the wire. The wire is so small that the atoms that make up the wire are lined up like people standing in line. Each copper atom has one electron in its outer orbit. Let us imagine that something tries to give an electron to the atom at one end of the wire. The only way that an atom can accept the electron is if it passes one on to the next atom at the same time. At any instant in time, each copper atom can only have one electron in its outer orbit. The second atom must also give up an electron to the third atom in order for it to accept an electron from the first atom. Since the atom at the other end of the wire cannot pass an electron to another copper atom, the passing on of electrons will not happen.
As you can see, the line of copper atoms must form a complete loop or closed circuit for the electrons to be passed on. When the loop is broken, the current stops flowing. This is referred to as an open circuit.
The Push
When we want to move an object, we exert a force on it. When we want to move electrons, we exert a special force called electromotive force or EMF. EMF is measured in volts (abbreviated as V). EMF can be produced by chemical reaction as in a battery. EMF can also be produced by an energy conversion device like a generator which converts mechanical power to electrical power, or a solar voltaic cell (solar cell) which converts electromagnetic radiation (sunlight) to electrical power. The devices that produce EMF try to move the electrons of the atoms within the device. In direct current (DC) devices, the device tries to push the electrons out one terminal and tries to suck them in on the other terminal.
The magnitude of the force exerted on the electrons is measured in volts and is usually referred to as the voltage, not the EMF magnitude. No current flows externally from the device that produces EMF unless there is a completed external circuit. Even when a battery is not connected to a circuit of highly conductive material, there is a circuit completed by the air around the battery. Since dry air is a very good insulator, the amount of current that flows is so small it is not measurable.
Ohm’s Law And Electrical Resistance
When we speak of the electrical resistance of a material, we are referring to the resistance of the material to pass on electrons. Electrical resistance is symbolized by the letter R for calculation purposes and is measured in ohms (abbreviated with the Greek letter). To measure the resistance of a material, we apply a voltage to the material and measure how much current flows as a result of the voltage. The resistance is then calculated by dividing the voltage V by the current I.
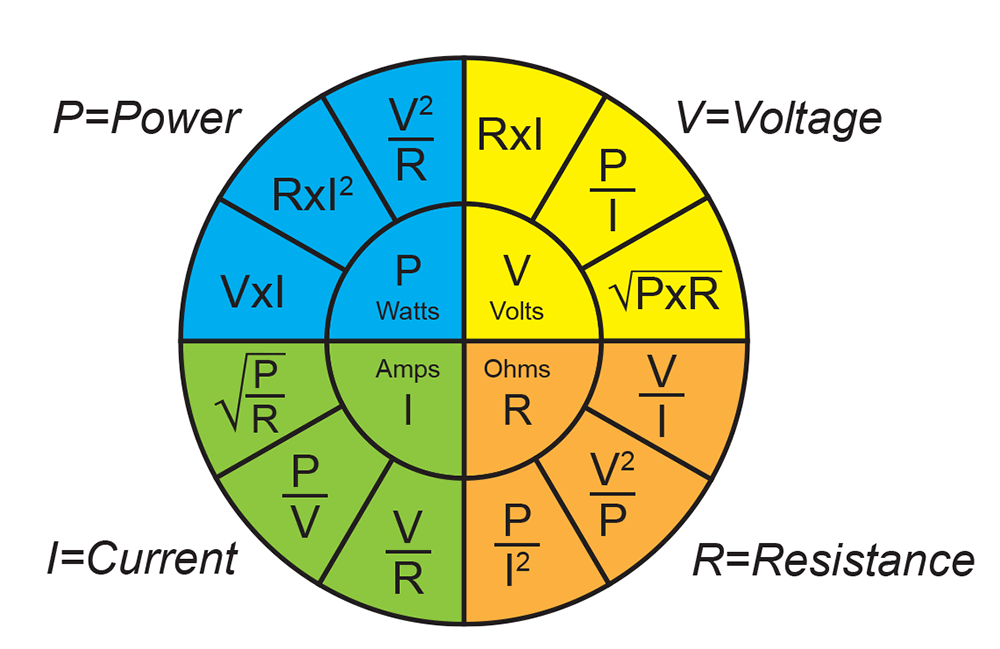
For calculation purposes, the letter I is commonly used to represent the current: R = V / I. This relationship between current, voltage, and resistance is known as Ohm’s Law because it was discovered experimentally by the German physicist Georg Simon Ohm around 1840. If we multiply both sides of the equation by I, we change the form of the equation to V = I x R. If we then divide both sides of the equation by R, we change the form of the equation to I = V / R. Now we have Ohm’s Law in three forms. I numbered each equation for future reference.
V = I x R (1)
I = V / R (2)
R = V / I (3)
If we know the value of any two of the three elements—current, voltage, or resistance—we can calculate the third. Later, I will crank through a few simple examples and talk more about resistance, but I first want to touch on power.
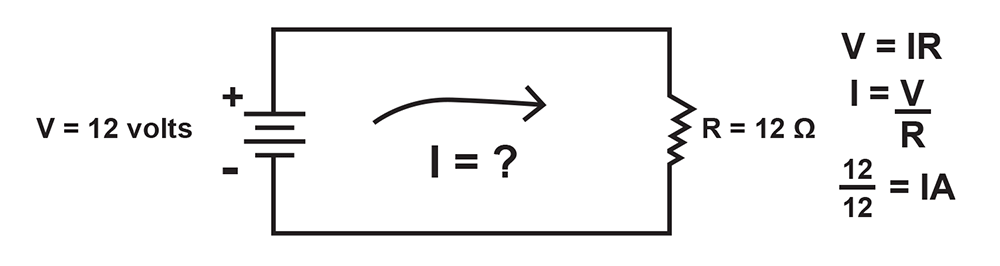
Power
In mechanical devices like internal combustion engines, power is the force the engine pushes on an object times the distance the object moves divided by the time it takes the object to move that distance. Power is symbolized by the letter P for calculation purposes.
Mechanical power is often measured in horsepower (abbreviated hp). For example, if the force necessary to keep a car moving at 30 miles per hour (44 ft./second) is 300 pounds, then the amount of power necessary is 300 lb. x 44 ft./sec.= 13,200 ft.-lb./sec. To convert to horsepower, we divide by 550. The power necessary to keep the car moving is 13,200 / 550 = 24 horsepower.
In electrical devices, power is measured in watts (abbreviated W). One horsepower equals 746 watts. If a one horsepower electric motor were 100 percent efficient, it would use 746 watts of power when delivering one horsepower of power. When the electrons move from one atom to another atom within a conductor, i.e., when current flows in a wire, heat is generated within the wire because of the passing on of the electrons. The power generated by the wire in the form of heat is the voltage across the wire times the current flowing in the wire: P = V x I.
Within an incandescent light bulb, there is a small piece of wire made out of tungsten. Because of its very high melting temperature (3380°C), tungsten works very well as a filament in light bulbs. If a light bulb is rated at sixty watts, that is the amount of power it uses when operated at its rated voltage.
How much current does a sixty-watt light bulb draw when operating at 120 volts?
If we divide both sides of the above equation by V, we change the form of the equation to I = P / V. Using this equation, we can calculate the current flowing in the light bulb. I = 60 W / 120 V = 0.5 A. To calculate the resistance of the filament, we combine the equations P = V x I and V = I x R, we get P = I 2 x R. If we divide both sides of the equation by I 2, we change the form of the equation to R = P / I 2.
Using this equation, the resistance of the bulb filament is 60 W / (0.5 A x 0.5 A) = 240 W.
Likewise, if we combine equations P = V x I and I = V / R, we get P = V 2 / R. If we multiply both sides of the equation by R and divide both sides of the equation by P, we change the form of the equation to R = V 2 / P.
Using this equation, the resistance of the bulb filament is (120 V x 120 V) / 60 W = 240 W.
Solving for V and I in the above equations, we create two additional equations. Now we have nine power equations relating power, voltage, current, and resistance. Using these equations and Ohm’s Law, if we know any two elements, we can calculate the other two.
P = V x I (4)
V = P / I (5)
I = P / V (6)
P = I 2 x R (7)
R = P / I 2 (8)
I = square root (P / R) (9)
P = V 2 / R (10)
R = V 2 / P (11)
V = square root (R x P) (12)
Standard Wire Sizes
Single strand wire sizes are identified by American Wire Gauge (AWG). The higher the gauge, the smaller the wire. Typical house wiring for receptacles is 14 AWG copper. 14 AWG has a diameter of 0.06408 inches. The next larger size after 1 AWG is 0 AWG, referred to as “one aught”1 and written as 1/0 AWG. The next larger size above 1/0 AWG is 00 AWG referred to as “two aught” and written as 2/0 AWG. I will talk about larger and multiple strand wires later.
Measuring Voltage, Current, And Resistance
Over the past one hundred years, various instruments have been used to measure voltage, current, and resistance. Today, the most common electrical test instrument in use is the digital multimeter because of its ability to accurately measure voltage, current, and resistance. We used to call them volt-ohm-meters (VOMs).
Note from the Technical Editor: Some things never change. This is true for understanding basic electrical theory. This article revisits articles provided to IAEI from 2004-2006 by David Young. May his words and wisdom live on and continue to provide you understanding of this topic.
Reprinted from IAEI Magazine. Author is David Young, “Basic Electricity Series,” from September/October 2004 through January/February 2006.









Find Us on Socials