Theory Terms and Definitions
The following definitions relate to basic electrical theory. It is important that installers and inspectors have a working knowledge of electrical theory. Such knowledge is often vital in determining proper size of conductors for circuits of various loads.
Volt — the unit of electrical pressure — is the pressure required to force one ampere through a resistance of one ohm; abbreviated as “E”, the first letter of the term electromotive force.
Ampere is the unit of electrical current that will flow through one ohm under a pressure of one volt in one second; abbreviated as “I”, the first letter of the term intensity of current.
Ohm — the unit of electrical resistance — is the resistance through which one volt will force one ampere; abbreviated as “R”, the first letter of the term resistance.
Watts is the unit of measurement of the energy flowing in an electrical circuit at any given moment. It is also the amount of work being performed in the electrical circuit. The terms watts or kilowatt have been used more commonly to express the amount of work done in the electrical circuit rather than the term joule. Watts is the product of multiplying volts and amperes and is sometimes referred to as volt-amperes. One thousand volt-amperes are referred to as one kilovolt-ampere or one kVA.
Ohm’s Law
George Simon Ohm discovered the relationship between current, voltage, and resistance in an electric circuit in 1826. He found, by experiment, that pressure equaled the product of current and resistance; this relationship is referred to as Ohm’s law. This law is the practical basis on which most electrical calculations are determined. The formula may be expressed in various forms and by its use, as in the three examples shown in figure 1.

Figure 1. Ohm’s law basic examples and application
If any two values are known, the third can be found by use of the formula. For example, if the resistance and the voltage are known, the current can be determined by dividing the voltage by the resistance. This can be valuable in determining the amount of current that will flow in the circuit to properly size conductors as well as overcurrent devices.
Horsepower. Mechanical power is usually expressed in horsepower and electrical power, in watts. The term horsepower originated as the amount of work a strong London draught (draft) horse could do during a short interval. It was also used to measure output of steam engines. One horsepower, abbreviated as “HP”, equals the work required to lift 33,000 pounds one foot (33,000 foot-pounds) in one minute. This is the same as lifting 550 pounds one foot in one second.
Often it is necessary to convert power from one unit to the other, and the equation in figure 2 is used to change horsepower to watts or watts to horsepower.

Figure 2. Basic HP formula
The HP formula applies to laboratory conditions as motors consume more power than they deliver. This is due to power being consumed as heat in the motor to overcome bearing friction, wind resistance and other factors. For example, a motor of 1 hp (746 watts) may consume nearly 1,000 watts, the difference being consumed in overcoming the factors already stated. The factor of motor efficiency must be considered to determine the true power for single-phase motors (see figure 3).

Figure 3. Basic power factor formulas
Watts Wheel
The Watts wheel has been developed and published in many manuals and in several variations to illustrate watts or power and its relationship to the elements of Ohm’s law. As shown in this text, it is accurate for dc circuits and for resistive loads of ac circuits where the power factor is near 100 percent or unity (see figure 4). Do not attempt to use it for motor loads, as both power factor and motor efficiency must be factored into the formula (see figure 3).
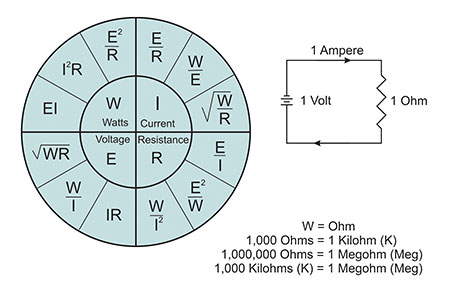
Figure 4. Watts wheel and Ohm’s law
In ac circuits, we use the term impedance rather than ohms to represent resistance of the circuit. Impedance is the total opposition to current flow in an ac circuit; it is measured in ohms. Impedance includes resistance, capacitive reactance, and inductive reactance. The last two factors are unique to ac circuits and can usually be ignored in circuits such as incandescent lighting loads and heater circuits consisting of resistive loads. A detailed explanation of capacitive reactance and inductive reactance is beyond the scope of this text but can be found in many excellent texts on electrical theory.
Ohm’s law and Basic Electrical Theory
Electrical current flowing through any electrical circuit can be compared with water under pressure flowing through a fire hose. Water flowing through a fire hose is measured in gallons per minute (GPM), and electricity flowing through a circuit is measured in amperes (A).
Water flows through a hose when pressure is exerted upon it and a valve is opened. Water pressure is measured in pounds per square inch (psi). An electrical current flows along an electrical conductor when electrical pressure is applied to it and a path is provided for the current flow. Just as the “pounds per square inch” (pressure) cause gallons per minute to flow, so the “volts” (pressure) cause “amperes” (current) to flow.
It takes more pressure to force the same amount of water through a small hose than through a larger hose. A small hose, with the same pressure applied to it in comparison to a larger hose, will pass much less water in a given period. It therefore follows that the small hose offers a greater resistance to the flow of water.
In an electric circuit, a greater electrical pressure (volts) will force a given amount of current (amperes) through a small conductor (resistance) than that required to force the same amount of current (amperes) through a larger conductor (resistance). A smaller-sized conductor will allow less current (amperes) to pass than a larger-sized conductor will if the same electrical pressure (volts) is applied to each conductor for the same period. The smaller conductor can only be assumed to offer greater resistance (ohms) than the larger conductor. Thus, we may define resistance as the “property of a body that resists or limits the flow of electricity through it.” Resistance is measured in ohms — a term similar to friction in a hose or pipe.
Excerpted from One- and Two-Family Dwelling Electrical Systems, 8th Edition. This book is available from www.iaei.org/web/shop or from Amazon.com.













Find Us on Socials