 Our interest in determining accurate onset to second-degree burn energy and its significance in computing the arc-flash boundary is focused on the prevention of injury to the skin of a human who might be exposed to an arc flash. During the last two decades different formulas have been proposed to calculate incident energy at an assumed working distance, and the arc-flash boundary in order to determine arc-rated personal protective equipment for qualified electrical workers. Among others, the IEEE Standard P 1584 Guide for Performing Arc-Flash Hazard Calculations1 and formulas provided in Annex D of NFPA 70E2 and CSA Z462 Workplace Electrical Safety Standard are the most often utilized in the industry to perform arc-flash hazard analysis. The formulas are based on incident energy testing performed and calculations conducted for a selected range of prospective fault currents, system voltages, physical configurations, etc.
Our interest in determining accurate onset to second-degree burn energy and its significance in computing the arc-flash boundary is focused on the prevention of injury to the skin of a human who might be exposed to an arc flash. During the last two decades different formulas have been proposed to calculate incident energy at an assumed working distance, and the arc-flash boundary in order to determine arc-rated personal protective equipment for qualified electrical workers. Among others, the IEEE Standard P 1584 Guide for Performing Arc-Flash Hazard Calculations1 and formulas provided in Annex D of NFPA 70E2 and CSA Z462 Workplace Electrical Safety Standard are the most often utilized in the industry to perform arc-flash hazard analysis. The formulas are based on incident energy testing performed and calculations conducted for a selected range of prospective fault currents, system voltages, physical configurations, etc.
Use of Incident Energy as a Measure of Burn Severity in Arc-Flash Boundary Calculations
The IEEE P 1584 was developed by having incident energy testing performed based on methodology described in the ASTM F1959-99 standard. The incident energy to which the worker’s face and chest could be exposed at working distance during an electrical arc event was selected as a measure for determining hazard risk category and calculating arc-flash protection boundary. The incident energy of1.2 cal/cm2(5.0 J/cm2) forbare skinwas selected in solving equation for the arc-flash boundary in IEEE P 1584.1Also, NFPA 70E2states that “a second-degree burn is possible by an exposure of unprotected skin to an electric arc flash above the incident energy level of 1.2 cal/cm2( 5.0 J/cm2)” and assumes 1.2 cal/cm2as a threshold incident energy level for a second-degree burn for systems 50 volts and greater.2IEEE 1584 Guide states that “the incident energy that will cause a just curable burn or a second-degree burn is1.2 cal/cm2(5.0 J/cm2).”1To better understand these units, IEEE P 1584 refers to an example of a butane lighter: “If a butane lighter is held 1 cm away from a person’s finger for one second and the finger is in the blue flame, a square centimeter area of the finger will be exposed to about5.0 J/cm2or1.2 cal/cm2.” However, IEEE P 1584 equations 5.8 and 5.9 for determining the arc-flash boundary can also be solved with other incident energy levels as well, such as the rating of proposed personal protective equipment (PPE). The important point to note here is that threshold incident energy level for a second-degree burn or onset to second-degree burn energy on a bare skin is considered constant value equal to1.2 cal/cm2(5.0 J/cm2) in IEEE P 1584 standard.
Flash Fire Burn Experimentations and Observations
Much of the research which led to equations to predict skin burns was started during or immediately after World War II. In order to protect people from fires, atomic bomb blasts and other thermal threats, it was first necessary to understand the effects of thermal trauma on the skin. To name the few, are the works done by Alice M. Stoll, J. B. Perkins, H. E. Pease, H. D. Kingsley and Wordie H. Parr. Tests were performed on a large number of anaesthetized pigs and rats exposed directly to fire. Some tests were also performed on human volunteers on the fronts of the thorax and forearms. A variety of studies on thermal effects have been performed and thermal thresholds identified for different degree burns. We will focus on second-degree burn as this is the kind of burn used to determine the arc-flash boundary in engineering arc-flash analysis studies.
Alice Stoll pursued the basic concept that burn injury is ultimately related to skin tissue temperature elevation for a sufficient time. Stoll and associates performed experimental research to determine the time it takes for second-degree burn damage to occur for a given heat flux exposure. Stoll showed that regardless of the mode of application of heat, the temperature rise and, therefore, the tolerance time are related to heat absorbed by the skin.3Results of this study are represented in figure 1 line (A) along with other studies discussed below.
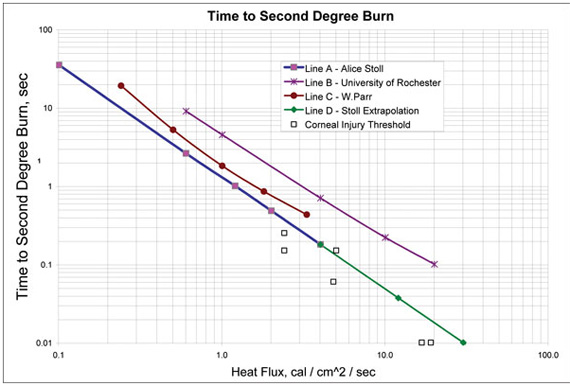
Figure 1. Stoll criterion time to second-degree burn for various incident heat fluxes on bare human skin
A. Stoll found that the results from her experiments could be predicted using Henrique’s burn integral.4Henrique and Moritz were the first to describe skin damage as a chemical rate process and to show that first order Arrhenius rate equation could be used to determine the rate of tissue damage.
In 1952, J. B. Perkins, H. E. Pease and H. D. Kingsley of the University of Rochester investigated the relation of intensity of applied thermal energy to the severity of flash fire burns.5 Comparing results of this study with those of Alice Stoll shows that a larger amount of energy is required to induce second-degree burn. Results of this study are represented in figure 1 line (B).
Figure 1 line (C) shows second-degree burn threshold as reported by Wordie H. Parr.6 The results were obtained by exposing skin to laser radiation and determining dose-response relationship for producing different grades of burns. Figure 1 shows that the Wordie H. Parr curve lies between those proposed by Alice Stoll and those proposed by the University of Rochester study. The explanation for these second-degree burn threshold differences could be interpreted by the fact that thermal injury depends on energy absorbed per unit volume or mass to produce a critical temperature elevation. Skin reflectance and penetration greatly influence this absorption. Also, heat conduction in tissue is far more efficient for small than for larger irradiated areas and exposure to higher levels of irradiance would be possible before injury occurred. Indeed, with extensive irradiation, injury would occur at far lower level of irradiance.7
After reviewing these three studies, it was concluded that the curve presented by Stoll is most suitable to evaluating the type of burn hazard expected with arc flash. Stoll’s study is a good choice because it is more conservative than the other two studies and, therefore, minimizes cases where the burn severity for a specific thermal flux exceeds the associated degree of burn, and is less open to criticism.
We have also included on figure 1 an arrangement of onset to corneal injury thresholds from CO2 laser radiation (see square markers on figure 1).7The data follows the trend similar to that observed by Stoll and others. The range of scatter in the data is thought to be mainly due to the use of different corneal image sizes.
Stoll’s results can be theoretically extended to include heat flux rates over 40 cal/cm2/sec experimentally observed, and they are represented by line (D) on figure 1. The observed and extrapolated data lines A and D can be expressed analytically as:
t = 1.3 * H-1.43, ( Equation 1)
where t is time to second-degree burn in seconds, H is heat flux in cal/cm2/sec.
As an example of using equation 1, the projected time to second-degree burn at a heat flux rate of 2 cal/cm2/sec is approx 0.5 sec. During this time interval the skin would be exposed to a total of 1 cal/cm2 incident energy (2 cal/cm2/sec x 0.5 sec = 1 cal/cm2), whereas at 30 cal/cm2/sec flux the time to second-degree burn is equal to 0.01 sec resulting in only 0.3 cal/cm2incident energy exposure but inducing, nevertheless, the same burn severity as the former less intense and more lasting exposure.
Discussion and Conclusion
Our understanding of the burn mechanism is not perfect or complete, but it is sufficient for the practical purposes concerned here. The important point to notice from figure 1 and equation 1 is that the degree of burn injury dependsnot only, and in fact not as much, on the total dose of energy received by the skin but also on therateat which the energy is received.
The concept of destructiveness of rapid liberation of heat is not new and is widely used in many industrial and military applications. Apart from total amount of heat released during an arc-flash event, it is the high heat flux rate that causes the gaseous products of arc flash to expand and potentially generate high pressures similar to most explosive reactions. This rapid generation of high pressures of the released gas constitutes the explosion. The liberation of heat with insufficient rapidity will not cause an explosion. For example, although a kilogram of coal yields five times as much heat as a kilogram of nitroglycerin, the coal cannot be used as an explosive because the rate at which it yields this heat is much slower.
Figure 2 shows onset to second-degree burn energy threshold adjusted for heat flux rate as a function of exposure time. The onset to second-degree burn energy threshold was calculated as a product of heat flux rate and time to second-degree burn as per the Stoll’s data from figure 1 lines A and D.
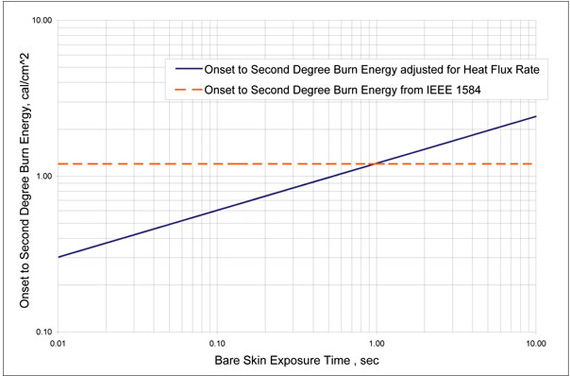
Figure 2. Threshold incident energy for a second-degree burn vs. exposure time
Figure 2 demonstrates thatthe threshold energy for a second-degree burn injury is not a constant but rather a variable. Note that the 1.2 cal/cm2 onset to second-degree burn energy for bare skin used in IEEE P 1584, NFPA 70E and CSA Z462 (dashed line on figure 2) intersects with the curve produced using the Stoll’s data at one (1) second point on figure 2. This observation supports the choice of Stoll’s curve we made for evaluating the type of burn hazard expected with an arc flash. For exposures lasting less than 1 second, the irradiance required for an injury would significantly increase as the duration of exposure decreased;however, the amount of incident energy required to cause second-degree burn would decrease. Equation 2 is an analytical expression for the threshold line represented by figure 2.
Eb= 1.2 * t0.3, (Equation 2)
where t is exposure time in seconds.Ebis threshold incident energy incal/cm2that needs to be released during the exposure timetto cause second-degree burn.
As an example of using equation 2, consider 1, 10 and 100 kA faults in 600-volt grounded switchgear with one (1) inch gap between conductors. Table 1 summarizes arcing current, incident energy and the arc-flash boundary (AFB) predicted using IEEE P 1584 empirical model. We deliberately assigned arc duration to 1, 0.1, and 0.01 seconds for the 1, 10 and 100 kA faults respectively, which is consistent with inverse nature of typical protective device time-current characteristics. Column F lists AFB values calculated using 1.2 cal/cm2 onset to second-degree burn incident energy recommended by IEEE P 1584 Guide. Column I lists AFB values calculated using onset to second-degree burn energy evaluated from equation 2 and published in column H.
Note that the amount of incident energy the person would be exposed to remains the same and equal to 2.1 cal/cm2in all three instances (Column D). The arc-flash boundary also remains the same when incident energy at AFB is assigned 1.2 cal/cm2value onset to second-degree burn energy as recommended in IEEE P 1584. Therefore, applying the same onset to second-degree burn energy for the above fault scenarios would make them appear to be of same severity. However, the arc-flash boundary drastically changes when incident energy at AFB is being evaluated using equation 2. AFB will now increase with an increase of the available fault current, predicted arcing current and heat flux released by an arc.
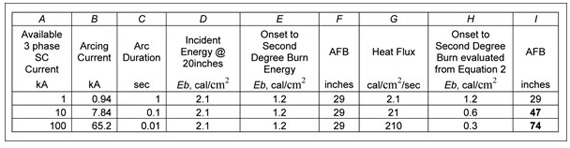
Table 1. This table summarizes arcing current, incident energy and the arc-flash boundary predicted using IEEE P 1584 empirical model.
Therefore, using onset to second-degree burn energy for bare skin exposure fixed to1.2 cal/cm2in calculating the arc-flash boundary for arc durations other than one (1) second is, as far as we are concerned, open to dispute and, in our strong opinion, heat flux rate should be factored-in when estimating skin damage imposed by an arc flash. Using the1.2 cal/cm2energy for exposure times less than one second will result in undervalued arc-flash boundaries while resulting in conservative but safe arc-flash boundaries for exposure times more than one (1) second. As the IEEE 1584Guidestates, theGuide’sequations (5.8) and (5.9)1can be used to calculate the arc-flash boundaries with boundary energy other than1.2 cal/cm2; and we believe the equations should be, in fact, solved for boundary energy computed using the equation 2 especially for cases when arc duration is less than one (1) second.
References
11584 IEEE Guide for Performing Arc-Flash Hazard Calculations. IEEE Industry Applications Society, September 2002.
2NFPA 70E Standard for Electrical Safety in the Workplace, 2012.
3Stoll, A.M., Chianta M.A, Heat Transfer through Fabrics. Naval Air Development Center, September 1970.
4Torvi D.A., A Finite Model of Heat Transfer in Skin Subjected to a Flash Fire. University of Alberta, Spring 1992.
5J. B. Perkins, H. E. Pearse, and H. D. Kingsley, Studies on Flash Burns: The Relation of the Time and Intensity of Applied Thermal Energy to the Severity of Burns, University of Rochester Atomic Energy Project, Rochester, NY, UR-217, December 1952.
6Wordie, H. Parr, Skill Lesion Threshold Values for Laser Radiation as Compared with Safety Standards. US Army Medical Research Laboratory. February 1969.
7IPCS. Lasers and Optical Radiation. World Health Organization, Geneva, 1982.














Find Us on Socials