A little bit of history is in order before we get into AC and DC circuit theory. In the latter part of the 19thcentury there were three principal players in the electrical generation and transmission industry. Thomas Edison, known as the “Wizard of Menlo Park” and most famous for his invention of the electric light bulb, was the main proponent of direct current (DC) transmission. George Westinghouse and Nikola Tesla were the main proponents of alternating current (AC) transmission. History documents this formative period in the development of electrical generation and transmission as the “War of Currents.”
Edison has been portrayed as the tireless inventor filing more than 1000 patent applications with the U.S. Patent Office. Since he was more of an inventor than a mathematician or physicist, he was not very receptive to the analytical complexities of alternating current. Tesla was quite the opposite in that he developed many theories concerning single-phase and polyphase systems. Westinghouse was an inventor like Edison, but he was also an engineer. He provided the financial backing for the development of a working AC network. It is noted in the literature that Edison went to great lengths to discredit AC power and its unsafe nature. He carried out many public relations campaigns by electrocuting animals with AC power. In the end, Westinghouse’s development of the transformer allowed alternating current to be the correct choice for power generation and transmission.
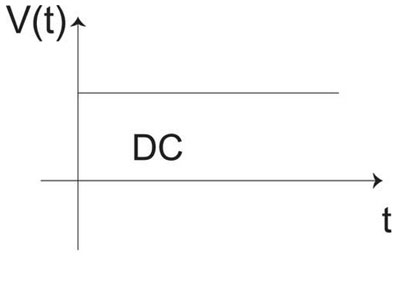
Figure 1. DC Waveform
Every time you start your vehicle, run a cordless drill, or use any type of electronic equipment you are using DC. The battery in your vehicle uses chemical energy to separate positive and negative charge thereby developing a potential difference between its terminals to produce 12 VDC to crank the engine. The battery in your cordless drill uses a similar mechanism to power the drill’s motor. The electronic equipment you use every day, excluding portable equipment, converts the incoming AC supply to DC through a process known as rectification. Figure 1 is an example of a constant DC waveform.
The lights in your office, the receptacles you plug devices in within your home, and the large motors in a manufacturing facility are examples of equipment that use AC. AC power is generated and distributed in the United States at a frequency of 60 Hertz. The AC waveform is time varying and uses a sinusoidal function to model its behavior. Figure 2 illustrates a sinusoidal AC waveform.
There are five electrical properties that have to be introduced in circuit theory to help with the analysis. These are resistance, capacitance, inductance, reactance, and impedance. The standard symbols for resistors, capacitors, and inductors are shown in figure 3.
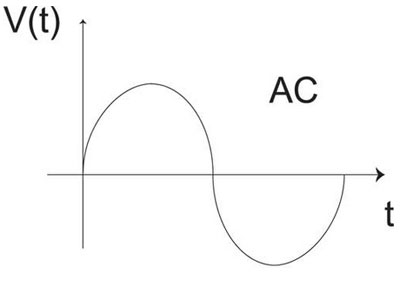
Figure 2. AC Waveform
Resistance (R)can be defined as the property of a material to oppose movement of charge or current flow. The unit of resistance is the ohm. Resistors are components that oppose current flow. Figure 4 illustrates a circuit with resistors in series and a circuit with resistors in parallel. It is important to note that in a series circuit the current is the same through each element, and in a parallel circuit the voltage is the same across each element.
Capacitance (C)can be defined as the property of a material to oppose any change in voltage across the material. The unit of capacitance is the farad. Capacitance occurs when two conducting materials are separated by an insulator. In a parallel plate capacitor two conducting plates are separated by an insulator known as a dielectric. The capacitor has the ability to block DC signals and pass AC signals. Under steady state conditions the capacitor acts like an open circuit to DC and a frequency selective device to AC. Figure 5 illustrates a circuit with capacitors in series and a circuit with capacitors in parallel.
Inductance (L)can be defined as the property of a material to oppose any change in current through the material. The unit of inductance is the henry. All conductors even those not coiled have some inductance. Under steady state conditions the inductor acts like a short circuit to DC and a frequency selective device to AC. Figure 6 illustrates a circuit with inductors in series and a circuit with inductors in parallel with no mutual coupling.

Figure 3. Electrical Components
Reactance or more specifically capacitive reactance (Xc) and inductive reactance (Xl) can be defined as the opposition to current flow these components present under AC conditions. The unit of reactance is the ohm. These devices change their reactance based on the applied frequency.
Impedance (Z) can be defined as the total opposition to current flow presented by the combination of resistance and reactance in an AC circuit. The unit of impedance is the ohm. Under steady state conditions impedance allows for the analysis of a complex AC network in the frequency domain using the same techniques that would be used in a simple DC circuit.
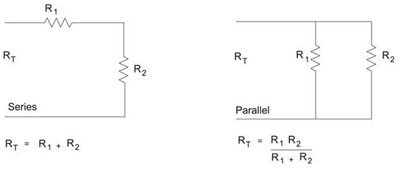
Figure 4. Resistor Circuits
Useful Theorems.We have already mentioned Ohm’s Law. Two other very useful network theorems are Kirchhoff’s Voltage Law (KVL) and Kirchhoff’s Current Law (KCL). KVL states that in the closed loop of a circuit, also called a mesh, the algebraic sum of the voltage drops and voltage rises equals zero. KCL states that the algebraic sum of current at a node, where a node is defined as a junction of three or more current paths, equals zero.
Five other network theorems that are extremely useful for circuit simplification and analysis are:
- The Superposition Theorem
- Thevenin’s Theorem
- Norton’s Theorem
- The Maximum Power Transfer Theorem
- Delta/Wye – Wye/Delta Conversion Theorem
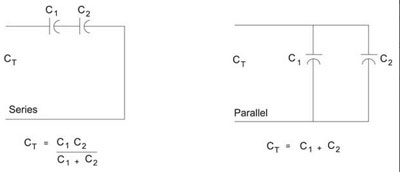
Figure 5. Capacitor Circuits
The Superposition Theorem allows you to solve complex networks with multiple voltage sources. Thevenin’s Theorem allows you to convert a complex network into a simple circuit with a Thevenin’s equivalent voltage source and a Thevenin’s equivalent series resistor. Norton’s Theorem allows you to convert a complex network into a simple circuit with a Norton’s equivalent current source and a Norton’s equivalent parallel resistor. These three network theorems are very useful in electronics applications. The Maximum Power Transfer Theorem states maximum power is transferred from the source to the load when the internal resistance of the load matches the internal resistance of the source. This theorem is very useful in power and communications applications. The Delta/Wye – Wye/Delta Conversion Theorem allows you to convert back and forth between a Delta-connected network and a Wye-connected network. This theorem is very useful in power and electronics applications.
This article provides an overview of basic circuit theory. The principles learned in DC circuit analysis with resistive networks can very readily be applied to AC networks with capacitors and inductors. Once the values of capacitance and inductance are converted to their corresponding values of capacitive reactance and inductive reactance at the specified frequency, the new values of complex impedance can be used to solve for circuit parameters with the same methods used in resistive networks.
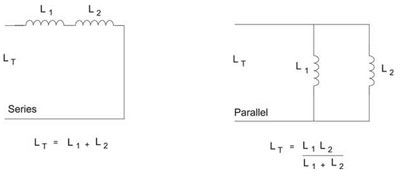
Figure 6. Inductor Circuits











Find Us on Socials